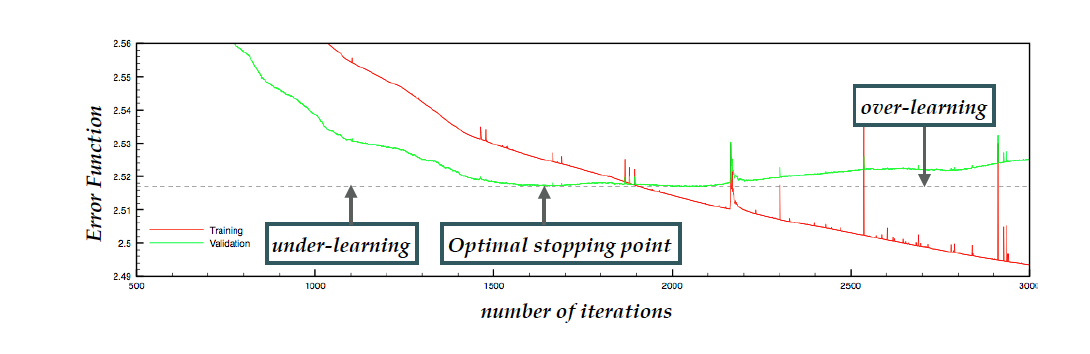
The cross-validation stopping strategy works as follows.

First of all, the input experimental measurements are divided into two categories at random, the training sample and the validation sample, typically with equal probability.

Only the former is used in the fit, while the latter plays the role of a control sample used to monitor and validate the training progress.

As shown in the figure above, a shorter fit would result in under-learning (where the NN has not properly learned yet the underlying law) while a longer fit instead leads to over-learning (where the NN ends up fitting statistical fluctuations).

The tell-tale sign of the latter is the increase of the validation increases (rather than the decrease) as the number of iterations increases, indicating that what is being learned in the training sample is not present in the validation one (namely the fluctuations).

When the optimal stopping point is defined as the global minimum of the of the validation sample, computed over a large fixed number of iterations we call the strategy “look-back”. Instead, if we stop after the validation no longer improves for a defined number of iterations we call it “patience algorithm”.  The technical details of the NNPDF stopping algorithm are described in the code documentation.