Closure testing
Fitting experimental data is often complicated by a number of factors unrelated to the methodology itself, such as possible dataset inconsistencies (either internal or external) or inadequacies of the theoretical description adopted.
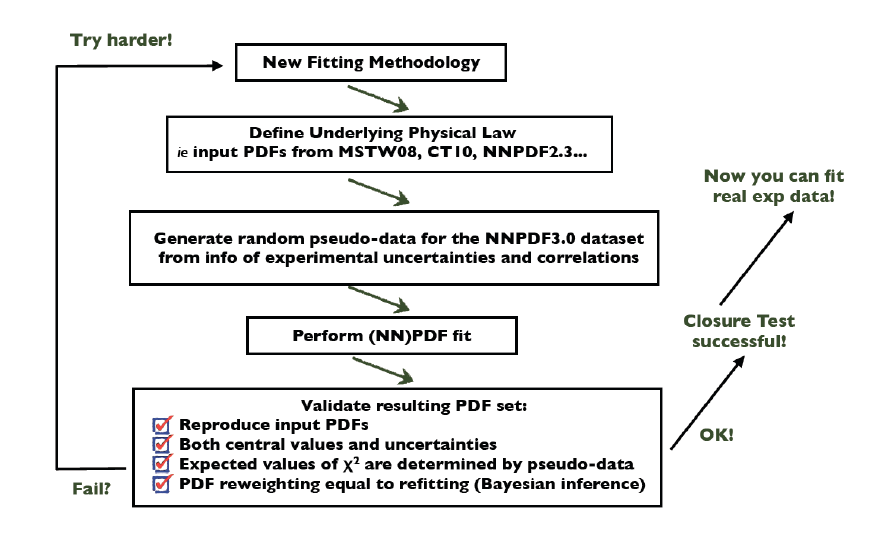
Therefore, it is far from optimal to assess the benefits of an specific fitting methodology by applying it to the actual data, while it is much more robust to test it instead in an analysis of pseudo-data generated from a fixed (known) underlying theory.
In these so-called closure tests, one assumes that PDFs at the input scale ![]() correspond to a specific model (say MMHT14 or CT14), generate pseudo-data accordingly, and then carry out the NNPDF global fit.
correspond to a specific model (say MMHT14 or CT14), generate pseudo-data accordingly, and then carry out the NNPDF global fit.
Since in this case the “true result” of the fit is known by construction, it is possible to systematically validate the results verifying for example that central values are reproduced and fluctuate as indicated by the PDF uncertainties, or that the ![]() values obtained are those that correspond to the generated pseudo-data.
values obtained are those that correspond to the generated pseudo-data.
Additionally, one can verify that PDF reweighting based on Bayesian inference reproduces the fit results, providing a further cross-check that the resulting PDF uncertainties admit a robust statistical interpretation.
In the figure above we show a flow chart indicating how a given fitted methodology can be closure tested in order to demonstrate the statistical robustness of its results.
