Neural Networks

In the NNPDF approach, the parton distribution functions (or the fragmentation functions) are parameterized at a low scale, around the boundary between the perturbative and non-perturbative regimes of QCD, namely Q_0 \simeq 1 GeV (the proton mass).

As opposed to other fitting approaches, where the PDF shape is parametrised in terms of relatively simple functional forms more or less inspired in QCD models, we use artificial neural networks (NNs) as unbiased interpolants.

This allows us to avoid the theoretical biases that can be incurred when specific model functional forms are adopted.

Note here that QCD provides only very limited guidance about the behaviour of PDFs at the input parametrisation scale Q_0, such as integrability conditions and the momentum and valence sum rules, and does not provide any further information on their x dependence at low scales.

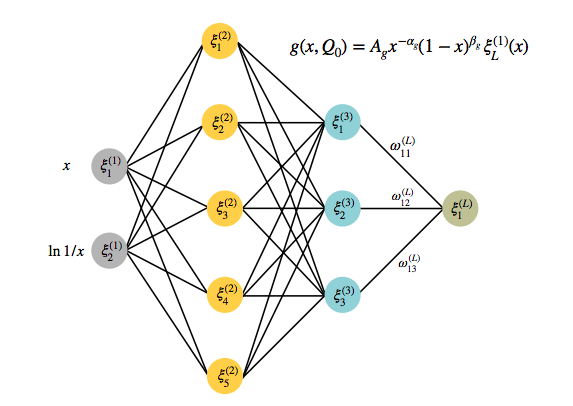
Specifically, in the NNPDF fits we use multi-layer feed-forward artificial neural networks (perceptrons) such as the one shown in the figure above.

This NN has a 2-5-3-1 architecture with two inputs (x and \ln 1/x) and one output neuron, which is directly related the the value of the PDF at the input parametrisation scale Q_0.

The activation state of each neuron is denoted by \xi_{i}^{(l)}, with l labelling the layer and i the specific neuron within each layer.

The values of the activation states of the neurons in layer l are evaluated in terms of those of the previous layer (l-1) and the weights \{\omega_{ij}^{(l)}\} connecting them as well as by the activation thresholds of each neuron \{\theta_{i}^{(l)}\}.

The training of the NN in this context corresponds to determining the values of the weights and thresholds that fulfill the constraints of a given optimisation problem.