Minimization

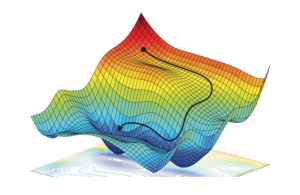
The training (also known as learning or optimisation phase) of neural networks is carried out using the gradient descent method in one of its versions such as back-propagation or stochastic gradient descent. In these methods, the determination of the fit parameters (namely the weights and thresholds of the NN) requires the evaluation of the gradients of \chi^2, that is,

(1)   \begin{equation*} \frac{\partial \chi^2}{\partial w_{ij}^{(l)}} \,\mbox{,} \quad \frac{\partial \chi^2}{\partial \theta_{i}^{(l)}} \,\mbox{.} \end{equation*}

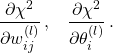
Computing these gradients in the NNPDF case involves handling the non-linear relation between the fitted experimental data and the input PDFs, which proceeds through convolutions both with the DGLAP evolution kernels and the hard-scattering partonic cross-sections as encoded into the optimised APFELgrid fast interpolation strategy.

The theory prediction for a collider cross-section in terms of the NN parameters reads

(2)   \begin{equation*} \sigma^{\rm \small (th)}\lp \{ \omega,\theta\}\rp = \widehat{\sigma}_{ij}(Q^2)\otimes \Gamma_{ij,kl} (Q^2,Q_0^2) \otimes q_k\lp Q_0,\{ \omega,\theta\} \rp \otimes q_l \lp Q_0 ,\{ \omega,\theta\}\rp \end{equation*}

where \otimes indicates a convolution over x, \widehat{\sigma}_{ij} and \Gamma_{ij,kl} stand for the hard-scattering cross-sections and the DGLAP evolution kernels respectively, and sum over repeated flavour indices is understood.

In the APFELgrid approach, this cross-section can be expressed in a much compact way as

(3)   \begin{equation*} \sigma^{\rm \small (th)}\lp \{ \omega,\theta\}\rp = \sum_{i,j=1}^{n_f}\sum_{a,b=1}^{n_x}{\tt FK}_{k,ij,ab} \cdot q_i\lp x_a,Q_0, \{ \omega,\theta\}\rp \cdot q_j\lp x_b,Q_0, \{ \omega,\theta\}\rp \,, \end{equation*}

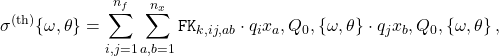
where now all perturbative information is pre-computed and stored in the {\tt FK}_{k,ij,ab} interpolation tables, and a,b run over a grid in x.